Why Are Query Plans Trees?

Looking at just about any database's EXPLAIN output will reveal that generally, queries get compiled into tree-shaped plans, rather than general cyclic graphs or DAGs. There are some exceptions to this. Any Datalog engine that compiles its queries into dataflow will generally need cycles. Snowflake's SIGMOD paper from 2016 remarks that they made the choice to use a push-based query engine partially in the interest of being able to process DAG-shaped query plans well.
Since cycles actually introduce additional computational power, I want to focus on the distinction between trees and DAGs. For the most part, trees are the norm. This isn't because DAGs aren't useful. In fact, they're very useful. It's pretty easy to construct SQL queries that would be able to make good use of a DAG plan:
WITH foo AS (some complex query)
SELECT * FROM foo a CROSS JOIN foo b
This kind of query has a natural DAG plan:
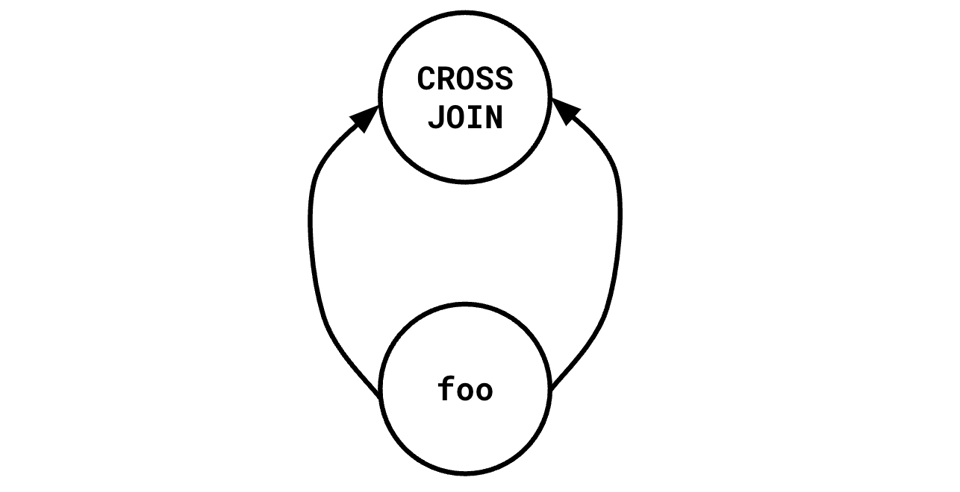
But this sort of thing needs to be constructed explicitly, with some resistance from the underlying DBMS. In Postgres, such a structure is an explicit optimization fence (and until recently, even referring to a WITH once introduced an optimization fence).
Some of the reason for this is that plans like this cause all kinds of problems for execution engines. I've written a bit about this in the past. There's another reason, however, which is that it makes optimizing queries objectively, quantitatively harder.
Background on Optimization
Consider the changemaking problem, where given a target number of cents, we want to figure out the smallest number of coins that will let us make that number. For some coin systems, such as the standard American 1,5,10,25 system, it suffices to use the obvious greedy algorithm and always take the largest coin that we can until we reach the desired amount. This isn't true for every coin system, though. If our denominations are 1,3,4, this strategy doesn't work (consider making 6).
What does work to solve this is to use dynamic programming. Define the following recurrence:
f(x) = infinity if x negative
f(0) = 0
f(n) = 1 + min(
f(n - 1),
f(n - 3),
f(n - 4),
)
and then go either up the chain, starting by computing f(0) and up until we reach the value we want, or down the chain, starting by trying to compute f(n) and resolving and caching all the dependencies until we reach our base case. This lets us solve this problem in O(n) time. We get to O(n) even though our recurrence branches, because we can re-use results across multiple paths.
Why does this work? How come I can re-use my computation of, say, f(3) across multiple ways of arriving at it?
The answer is that we can do this because this problem obeys what is called the Principle of Optimality (I won't be abbreviating this) (this was another name I was considering for this newsletter).
The Principle of Optimality goes like so:
A problem broken up into subproblems adheres to the Principle of Optimality if, in any optimal solution to the original problem, the solutions to all of the subproblems are also optimal.
Concretely: if I am trying to make 3 cents, the best way to do so is always the same, independent of context.
This means that if I encounter the task of making 3 cents in two different contexts, I can re-use the solution between the two. The Principle of Optimality is what makes dynamic programming work.
Problems that obey this are quantitatively easier to solve than those that don't. For example, an instance of the Traveling Salesman Problem can be broken up into smaller instances of itself, by taking a subset of the cities that we want to tour. However, given optimal tours over those sets of cities, one cannot easily derive an optimal tour over the larger set of cities. This is because the Principle of Optimality doesn't apply here: each subproblem must be considered in context.
Application to Planning
A large part of query planning is concerned with "optimization." And I mean that in both senses, the programmer sense, and the mathematical sense. Here, when I say "optimization," I'm referring to the mathematical sense: finding the "best" object according to some criteria.
In a tree-shaped query plan, subtrees of an operator adhere to the Principle of Optimality. This isn't anything deep:
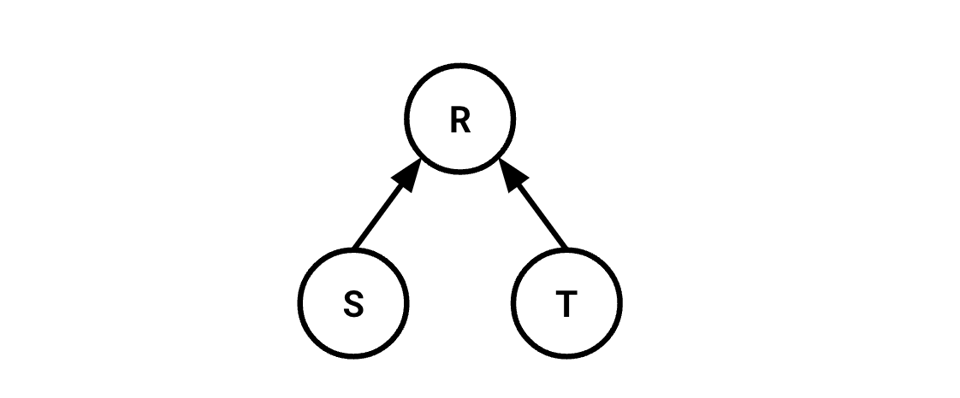 It just says that if, to compute
It just says that if, to compute R, I need to compute S and T, then it suffices to consider S and T in isolation, compute them, then compute R.
This makes optimization of the whole tree "easy," in some sense. Optimizations can be local and don't need to be concerned with the structure of the tree in the large.
Consider, now, if the tree can be DAG shaped:
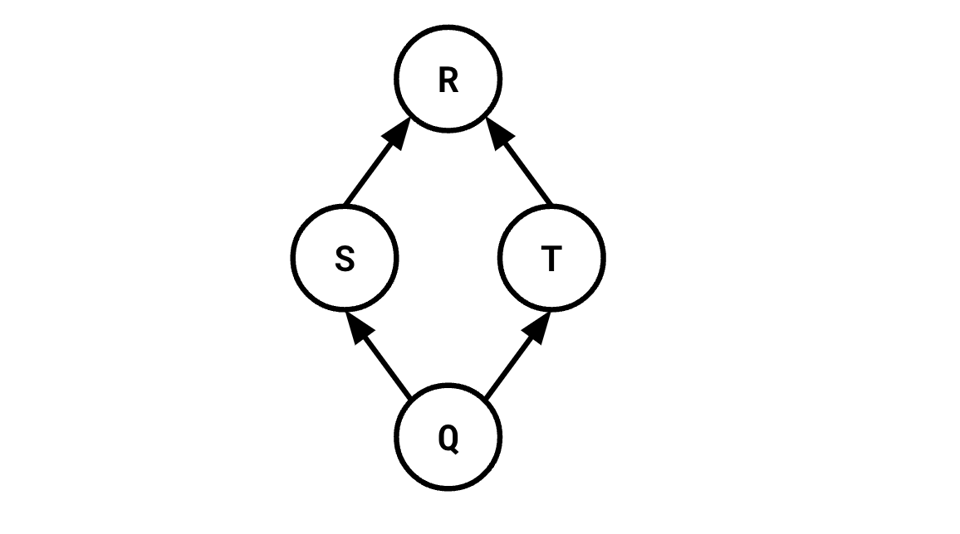
That is, to compute S and T, we also need to compute Q.
This no longer adheres to the Principle of Optimality: say we attempted to transform the computation of T, so instead of being derived from Q, it was derived from some other subtree W:
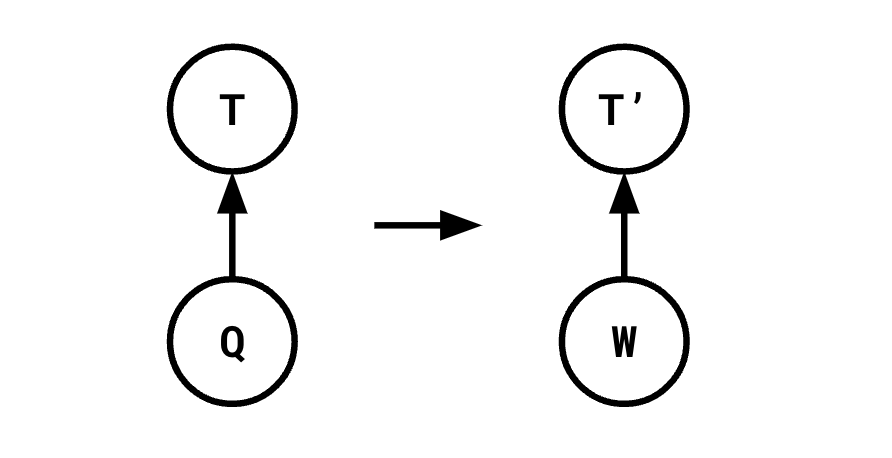
In a tree shaped graph, it would be very easy to determine the cost of such a transformation. It's
cost(T') + cost(W) - cost(T) - cost(Q)
since we're now computing T' and W instead of T and Q. However, in our DAG above, this calculation is wrong! Because we still need to compute Q in order to compute S. And there was actually no way for us to know that without having a more global view of the query we're optimizing.
Conclusion
Again, I want to clarify. I don't mean we can't "do optimizations" on such a plan. Of course, we can. But we have lots of mathematical guarantees about trees that we do not have about DAGs. And that makes things hard. Not impossible—we solve hard problems in day-to-day software all the time. Ordering joins even in a tree setting is NP-hard, and we manage to do that adequately most of the time. But there's still a quantitative leap in the difficulty of the problem being solved here, both in terms of computational complexity and software complexity.
