Independence and The Futility of Cardinality Estimation

The official NULL BITMAP position is that query planners exist to approximate domain knowledge. That is, they're tools to replicate the knowledge of an expert in the domain of whatever your database happens to be storing data about.
It's easy to take this to mean that this is a tool of making smart decisions, but very often this is really mostly a safety valve so that the decisions we make are not stupid.
If I'm doing a two-way join between a table that has ten million rows and a table that has ten, it would be very bad if I picked arbitrarily which one to use as the build side of my hash table, and wound up using the one with ten million. Query planners are very very good at making sure we don't pick incorrectly in simple situations like this.

Of course, we also have more taxing asks of query planners: if I compose several views to come up with an analytical query that joins sixty tables, I expect it to make okay decisions there too. This is a much harder problem though. Primarily because as we join each of those tables, our guesses as to how big they are tend to get more and more inaccurate, and as they do so, our decisions get worse and worse, and nobody does a particularly good job of mitigating this. See How Good Are Query Optimizers, Really?. This paper is also notable for introducing the Join Order Benchmark (JOB).
The classic takeaway from the above paper is that query optimizers chronically underestimate the size of joins:

Which might be surprising, intuitively. I think I'd expect an error distribution centered on the true value, or something.
A way to think about why this might be true is that one of the standard tools (a standard tool not because it's effective, but because it's one of the only ones we have) for estimating the size of joins is the Attribute Value Independence assumption, or just AVI.
 My newsletter software doesn't allow me to embed math notation. Which is probably saving me from myself. But it will make describing this somewhat awkward so bear with me.
My newsletter software doesn't allow me to embed math notation. Which is probably saving me from myself. But it will make describing this somewhat awkward so bear with me.
The selectivity of a predicate p over a relation R is defined as the number of rows in R that satisfy p divided by the total number of rows in R:
def sel(p, R):
return R.filter(p).count() / R.count()
The thing we tend to want to know is R.filter(p).count(), and so we generally start from trying to estimate the value of sel(p) (from which we can compute the size of the filtered relation as R.count() * sel(p)).
AVI states that if I have two predicates, p1 and p2, over some relation R, then sel(p1 AND p2) = sel(p1) * sel(p2). This is really just the notion of independence from probability and statistics applied to predicates and relations.
It should be noted that this is very obviously untrue for a lot of things, like where p1 = p2, or p1 = NOT(p2), or something. But the point of it is to give us some kind of concrete rule to use to infer things about conjunctions of predicates.
A pair of positively correlated predicates have sel(p1 AND p2) > sel(p1) * sel(p2), while a pair of negatively correlated predicates have sel(p1 AND p2) < sel(p1) * sel(p2)
The fact that we chronically underestimate the rows counts of queries suggests that empirically, it seems as though predicates are more likely to be positively correlated than negatively so. At least in the benchmarks we have.
To see why this might be true, look at this excerpt from query 30c of the Join Order Benchmark:
AND k.keyword IN ('murder',
'violence',
'blood',
'gore',
'death',
'female-nudity',
'hospital')
AND mi.info IN ('Horror',
'Action',
'Sci-Fi',
'Thriller',
'Crime',
'War')
If these two predicates are positively correlated, and on inspection it seems like they are likely to be, AVI will lead us to chronically underestimate cardinalities for this query.
What makes this such a persistent problem, and not just something we could track additional statistics for, is that sometimes these correlations only show up after joining tables. We might have two base tables whose attribute values look uncorrelated, but after joining them, correlations appear.
One really good paper on the topic of if this whole deal is salvageable is How I Learned to Stop Worrying and Love Re Optimization. In this paper they ask not just the question of "can we make cardinality estimation better," but "how much better would we have to make it in order to improve the quality of our query plans?" The paper is nominally about an approach to re-optimizing query plans after executing parts of them, which is interesting, but I think this analysis is the real gem of this paper.
To do this, they modify PostgreSQL to be able to perfectly compute the size of joins up to various sizes:
We explore how the quality of improved cardinality estimates impacts the execution time of the workload. To get a rough estimate, we define the construct of perfect-(n) as a version of PostgreSQL where the cardinality estimator is given an oracle for cardinality estimates on joins of n tables and fewer. This means that perfect-(n) has an oracle for a subset of cardinality estimates of perfect-(n + 1). To estimate the cardinality of joins of more than n tables, the default PostgreSQL cardinality estimate is used. For example, to make an estimate of a join of 5 tables in perfect-(4), the cardinality estimator receives as input perfect base table cardinalities and join cardinalities of up to 4 tables, but otherwise uses its default estimation techniques including independence and uniformity assumptions. The quality of estimates for joins of 5 tables, are, on average better with perfect-(4) than perfect-(3), etc. Perfect-(1) gives only perfect base table cardinality estimates. Since the there are at most 17 relations in JOB perfect-(17) has perfect cardinality estimates.
Figure 2 shows the end-to-end runtime of the executing all queries in the JOB with perfect-(n) for increasing values of n. We find perfect estimates on base tables, pairs of tables, and triples give virtually no benefit to benchmark execution time. Surprisingly, any method of improving cardinality estimation that does not achieve estimates better than perfect-(3) can expect to achieve nearly no improvement to benchmark execution time. We discuss why this is the case in following sections.
They later have the following diagram, showing the benefit of perfect-(n) for various n:
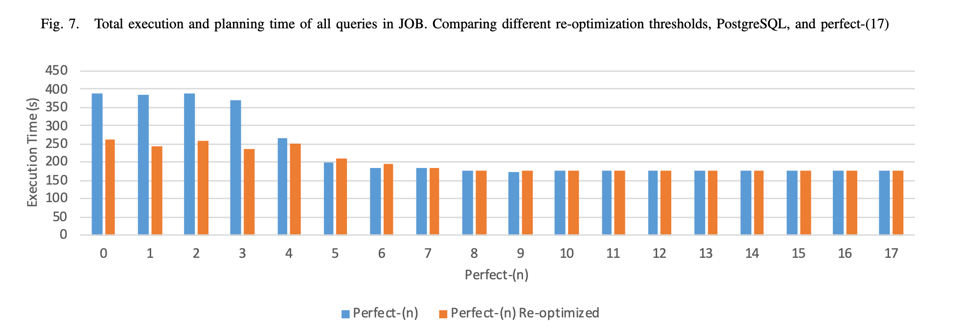
They interpret this to mean that for things to improve noticeably, we'd have to get as good as perfect-4. The rest of the paper discusses why they think that this is actually quite a high bar to clear, and I think it's a good read if you're into that sort of thing.
It's a good rule of thumb, I think, that query planners are liable to underestimate the sizes of joins. This notably makes them more optimistic than might be ideal.
