Thoughts about what worked in math circles
Thoughts about what worked in math circles
After about 7 months of math circles with a group of 7- turning 8-year-old boys and girls, I decided to take a break to breathe and reflect on what worked and what didn't.
It's interesting how big a gulf there is between what math topic you think will be interesting to a 7-year-old and what actually captures their attention. Let me start by giving some examples of things I thought would catch their interest but flopped.
- The game SET.
- Fold-and-cut puzzles.
- Geometry snacks.
- Cutting a Mobius strip.
- Tessellations (Tooti Tooti, pdf link).
- Prime Climb.
- Making flexagons.
- Ruler and compass constructions.
Things I didn't think they'd like but they loved:
- Knights and Knaves puzzles, and more generally any topic about propositional logic (blue-eyed islanders.
- Manually scheduling a round-robin tournament's worth of sports games, trying to minimize the latency of the entire tournament. (I originally phrased it as a soccer tournament, but that week the kid who loves soccer the most didn't show up, and so it turned into a DANCE competition, which was much more fun)
- Seven bridges problems, and trying to find the smallest "impossible" bridge problem.
- Trying to figure out who is better at penalty kicks based on counts of scores/misses.
- Coming up with your own Pascal's triangle-type pattern.
And then there were the problems I thought they would love, and they did.
- The Function Machine game (guess a function given the ability to query it as a black-box)
- Variations of Nim.
- The Turing Tumble.
- Fair cake cutting (with real cookies and oddly-distributed toppings).
- Game theory games like Prisoner's dilemma and Chicken.
- Making mocktails for 3 people, given a recipe for 1 drink, and again with a recipe that serves 5. (fractions practice). Measurements were in quarters of ounces.
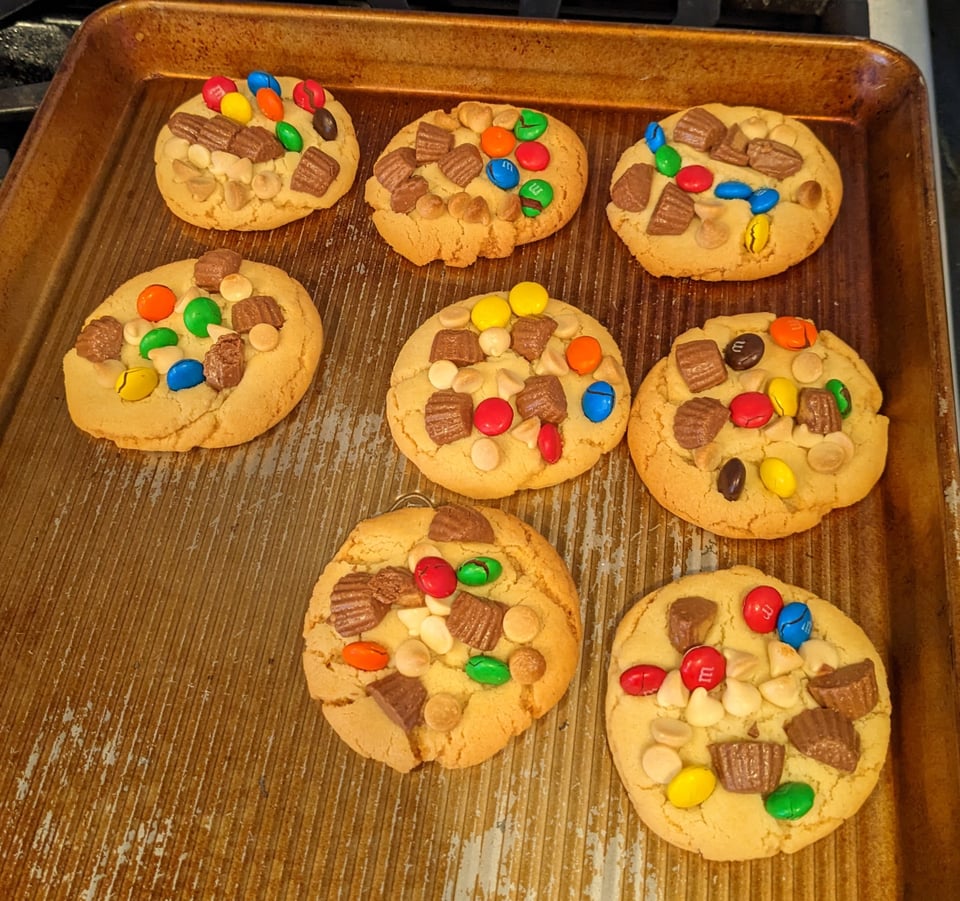

Back in 2019 I wrote an article, Attention spans for math and stories in which I described how I have used storytelling with kids of various ages (not in a math context) to get them participating in activities and feeling welcome in a group. I tied it back to math,
To have good mathematical content revolving around stories, mathematicians should learn to tell stories well.
Somehow, though, my story-telling game was off during some of my math circles. I think through all my reading and learning about math circles, I had internalized a different viewpoint. That viewpoint, roughly speaking, is that the math should speak for itself. Much math circle literature seems to suggest that a facilitator should start with an open-ended mystery (like, "can you draw a perfect shape?") and then sit quiet until the participants start asking questions and exploring on their own (in this example, maybe discovering ruler and compass constructions).
I suspect this might work with an older group of students, or a group of students who have already bought into math in some sense. I know, for example, that many parents who find math circles are desperately searching for resources because their kid's math ability is beyond their comprehension. Some of these kids are believed to be on the autism spectrum as well.
The group I worked with were as typical upper middle class kids as you could find. They came to math circle after soccer practice. When they got bored during the circle they goofed off and roughhoused. Though they had never played "Among Us," they constantly called things "sus." More importantly, they just didn't care about number patterns unless it was couched in a more engaging format. Geometry was a complete dud, because it's even harder to come up with stories about arbitrary figures with shaded regions you want to find the area of. They didn't think tessellations were pretty. And they didn't have the dexterity required to make enough cuts and folds to construct objects out of paper, so they ended the fold-and-cut and flexagon activities feeling frustrated.
But the idea that there are two people, one of whom is a ROTTEN LIAR, and you have to figure out who is the liar based on the clues in what they say? That's gold. For that knights and knaves puzzle, I wrote down the phrases Alice and Bob said on pieces of paper, taped them to plastic straws, and held them up like signs. The first puzzle was:
- Alice: Bob is a liar!
- Bob: Neither of us are liars.
The kids all jumped to say who they thought was the most "sus", and they predicted that Alice was suspicious for blaming Bob. With a bit of discussion, they realized that they can't both be telling the truth because their claims are mutually contradictory (though they didn't have the word for this and often called it "opposites"). Then we talked about how many possibilities there are. First they thought 2, then 4. It's 4: two liars, liar truth-teller, truth-teller liar, and two truth-tellers. Then we proceeded to inspect each option, and after a while they agreed that the only possibility was that Alice was telling the truth and Bob was lying (correct!).
Then an interesting thing happened. As I moved on to the next knights-and-knaves puzzle they asked if they got the first one right. And I said, "well, do you think you got it right?" One boy admitted he wasn't entirely certain, and then we all agreed to keep thinking about it until we were convinced by the proof. So it was planting the seed: how do you know if you've truly proved something? Later in that session he remarked to one of the girl's comments, "No, we already proved that case!"
After the months of weekly sessions, however, I think the kids are warming up to the idea of the math speaking for its own sake. While I led the Seven Bridge of Konigsberg problem with a story, they quickly discarded the story and focused on the challenge. And in a later session they asked to revisit it because they wanted to try to find the "smallest impossible bridges problem." Indeed, they did! While we didn't solve the original problem, the idea of simplifying a problem, making it smaller and smaller until you can solve it, and then gradually adding back complexity, was clearly on display those weeks.
And though they hated flexagons, for an "end of the session" gift I made them each a hexaflexagon from a printed template which critically had bright, distinct pictures on each face. Weeks later, one girl's dad told me that she is obsessed with it, only recently discovering the sixth face. I let him know that you can draw a map of the flexagon's movements, much like the Seven Bridges maps we drew, to get a clear picture of the whole configuration space. I have yet to hear back whether they were able to figure it out.
So I have hope that this group can graduate to appreciating the math for its own sake. But if I were to start with a new group of kids who had no a priori love of math, I'd have to be a bit more deliberate in framing the problems in engaging stories.