The seven specification ur-languages
A brief overview of the formal specification landscape
Last week Madhadron's 2021 piece The seven programming ur-languages went viral. One I saw a lot was "where does TLA+ and Alloy fit into this?"
Hoo boy.
I've been dreading this one. You see, TLA+ and Alloy don't fit into any of the programming ur-languages, because they aren't programming languages. They are specification languages (SLs) and are designed for modeling systems, not implementing them. While there's a lot of intermixing, SLs come from a different lineage than PLs and we need to treat them separately.
So, someone has to write "the seven specification ur-languages", and I really don't want to be that person for three reasons:
- Taxonomy is a fool's errand. All taxonomies are broken, full stop. Your categories are gonna be completely wrong and everybody's going to argue over every single thing. There is no such thing as a fish.1
- I'm not remotely qualified to do this. Sure I've toyed with a few different formal specification languages before, but I've only been paid to do two of them.2 Ideally I'd want to be competent in five or six and also consult several experts before trying to categorizing things.
- Nothing is easy. At least with programming languages you've got a bunch of online docs and "hello world"s for comparisons. Everything in the formal methods world is squirreled away in papers and 60 dollar books.
OTOH, a first-draft taxonomy is better than no taxonomy, it's a topic I'm interested in, and I've rabbit-holed much dumber things before. Some caveats before we start:
- The title just mimics madhadron's piece. It's more accurate to call it the seven ur-formalisms, as we're talking about the mathematical concepts people used to model systems. Most end-state specification languages use several of these ideas in combination. Also it's not so much "ur-" as "archetype".
- This is just about specification languages, not formal verification. So no Agda, Idris, Lean, or SPARK. That roundup can come some other time.
- I spent a day on research and writeup. That really isn't enough time to either research or explain things well, but I have a lot of other stuff I need to do this week.
- I have no idea how this ended up longer than the original piece.

The Seven Specification Ur-Languages
1. Guarded Command Language
Invented by Edsger Dijkstra in 1975, this is basically a way of adding nondeterminism to pseudocode.
if
:: x < y -> x := y
:: y < z -> y := z
fi
If only one of the guard clauses is true, then it's a standard if statement. If more than one is true, one command is selected nondeterministically. Either x := y or y := z will happen, but not both. Multiple commands can have the same guard, which would lead to a random selection.
Dijkstra used this to abstract implementation details from algorithms. Here's how he defines "Euclid's Algorithm", which finds the greatest common denominator of X and Y:
// Euclid's algorithm
x := X, y := Y
do
:: x > y -> x := x - y
:: y > x -> y := y - x
od
He then showed that how this could refine to multiple different versions of the code.
I don't think GCL is used by itself much because the most common goal of specification is modeling a concurrent system, and while you can do that with purely nondeterminism primitives, you also want to some concurrency primitives too. But SLs still use GCL as part of their semantics, the most popular of which is Promela/SPIN.3 PRISM also uses GCL for probabilistic modeling: each guard is associated with a set of weighted commands, letting you compute the likelihood of reaching any given state.
2. Relational Algebra
In math the basic collection type is the set, collections of unordered unique elements. From sets, we build "functions", a mapping between two sets where each input maps to exactly one output. If we generalize functions, we get relations, which map each input to any number of outputs.4 A relational algebra, then, is a collection of rules and operations for manipulating relations, like "lookup".
The most famous relational algebra by far is Codd's relational model of databases. But it's also really prevalent in formal specification because it allows very nicely for manipulations with constraints. For example, take the structure:
- Each theatre seat may be sold to at most one customer
- Friends are customers
- If the show is a premier, all sold seats must be friends of the theatre
Here's how we can represent that all relationally:
schema BoxOffice {
types {Status, Customer, Seat}
vals {
status: Status
friends: set of Customer
seating: Seat -> Maybe Customer
}
properties {
status = "premier" => range(Seat) subset friends
}
}
The approach represents statics elegantly but struggles a little with modeling change. We have to do something tricky: first recognize that BoxOffice itself is a type with its own relations, and then define a "change" as a relationship between two BoxOffices.
schema System {
states: set of BoxOffice
init: BoxOffice
purchase: BoxOffice -> BoxOffice
}
properties {
forall b -> b': purchase {
some seat: Seating, c: Customer {
no b.seating.seat
b'.seating = b.seating ++ (seat -> c)
// don't change anything else
b'.status = b.status // etc etc etc
}
}
}
This example was adapted from Using Z (pg. 179). Z (pronounced Zed) was the first relational specification language, and arguably the first SL to see "significant" use by other people. Nobody uses Z anymore for much the same reasons we don't use COBOL and ALGOL: we learned lessons and made better languages.
The relational model is good for structure but really benefits from some extra change semantics. One descendant, B (not pronounced Bed but should be), adds state machine semantics. This is later refined with Event-B, which we'll talk about later. Another descendant, Alloy, used to hew closer to the pure relational model but recently added temporal logic. There was much rejoicing.
Speaking of temporal logic:
3. Temporal Logic
You know the usual example of a deductive proof?
- All men are mortal
- Socrates is a man
- Therefore, Socrates is mortal.
This only lets us work with certainties. Philosophers also like to manipulate uncertainties:
- AS FAR AS WE KNOW, all men are mortal
- WE ARE SURE Socrates is a man
- Therefore, Socrates is— AS FAR AS WE KNOW— mortal.
That gives us modal logic, regular logic augmented with "definitely" (□) and "possibly" (◇). There are different interpretations of what "definitely" and "possibly" are actually about, leading to different modal logics. One of these interpretations is that "definitely" means "all the time" and "possibly" means "some of the time". This gives us some flavor of temporal logic.
In 1977, Amir Pneuli invented linear temporal logic (LTL) and applied it to formal specification. Temporal logics quickly get popular because they are very good at specifying system properties. Here's how to say "all seats are eventually sold:
sold(seat) = some c: Customer:
(seat -> c) in seating
property { all s: Seat | ◇sold(s) }
And here's how to say 1) "eventually we're sold out" and 2) "all seats are eventually sold and stay sold":
property { ◇(all s: Seat | sold(s)) }
property { all s: Seat | ◇□sold(s) }
Because of this flexibility, you often see SLs use one notation for their system modeling language and then use some kind of temporal logic for expressing the properties of the system. SPIN and PRISM both do this: they use GCL for expressing the system and then LTL for expressing the properties of the system.
Other SLs use temporal logic for both modeling and properties. TLA+ is the most famous instance here. But people also write entire systems in LTL (or a sister temporal logic, like Computation Tree Logic).
4. Process Calculi
(Everything past this point is much shakier ground and why this is a newsletter and not a blog post, despite being 2500+ words.)
Process calculi are a family of approaches to modeling concurrency as a collection of independent, interacting "processes". Process here doesn't mean an OS process, but any kind of computational entity with local state. The goal of the calculus is to come up with rules for how the processes share information, so that we can infer properties about the global system, such as if it can deadlock or not.
mtype = {ok, already_sold, err};
chan buy = [1] of {Seat};
chan resp = [1] of {mtype};
active proctype Customer()
{
start:
Seat choice; // arbitrary seat
buy!choice; // write `choice` to `buy` channel
do
:: resp?ok -> break; // read ok from `resp` channel
:: resp?already_sold -> goto start; // etc etc
:: resp?error -> break;
od
}
(Notice that we don't need to define the server in the same place, as long as we can define the channels that it uses. This arguably makes processes more composable than raw temporal logic or relational models.)
Process calculi are especially interesting because, unlike prior discussed methods, they're also used by programming languages! Most famously Tony Hoare's Communicating Sequential Processes (CSP) inspired Go channels, while the Actor Model is used in Erlang and Pony. Even if you aren't using something with native processes you can often find a framework like Akka which implements a calculus at the library-level.
There's also a long history of using process calculi for abstract modeling. FDR4 directly checks CSP specifications and P is based on the actor model. SPIN and mCRL2 have their own homegrown calculi.5
5. State machines
A state machine is a peculiar type of system. System changes are organized into "transitions" between states, which have conditions and effects. If multiple transitions are available, the system can choose which one to take.
state Online {
on Powerbutton(soft?) {
if soft? {
save_everything();
}
goto Offline;
}
}
State Offline {
on Powerbutton(_) {
goto Online;
}
}
Now this looks a whole lot like guarded command language, and you can implement a state machine purely with GCL. The difference is more about the role in modeling. In languages with GCLs, the guarded commands define local nondeterministic procedures, like "add one or decrement one." In languages with state machines, the state machine decides the overall structure of the system.
State machines are the closest thing FM's got to a paradigm, and it's arguably the paradigm. There's a joke in formal methods that no matter what language you start with, you're going to end up with a state machine. They just work so well for modeling complex systems, and they implement well, too.
Languages with native state machine syntax include Event-B (pg 12), NuSMV, and P. Other SLs might not have syntax but you'll handroll state machines anyway. There are also formalized extensions of state machines, like Harel statecharts and Labeled Transition Systems, that add additional features. Statecharts are cool, check em out.
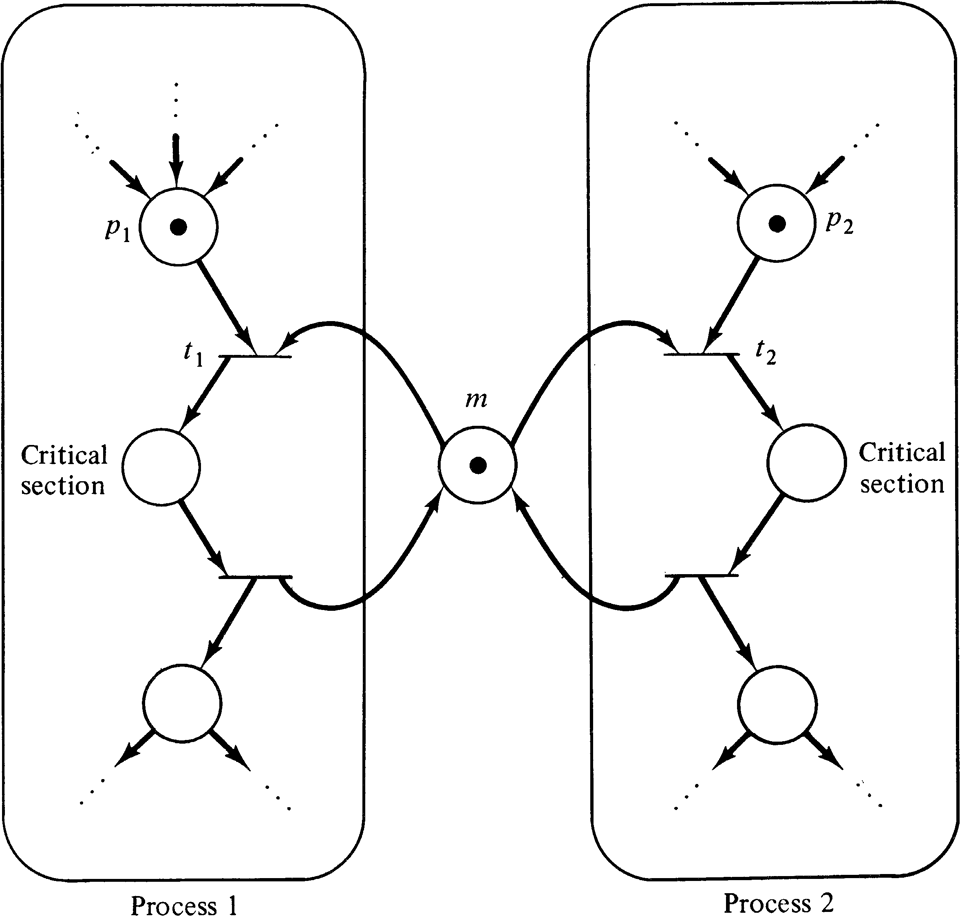
6. Petri nets
This is arguably just another extension of state machines, but it evolved separately and is used separately and is worth discussing separately.
The circles are "places" and the bars are "transitions". A transition is "live" if every inbound circle has a dot in it. When a live transition "fires", remove a token from every inbound circle and place a token in every outbound circle. If multiple transitions are live, any of them can fire. It's a little more complex than that but not much more complex. To my understanding people in process and chemical engineering used Petri nets before they migrated over to CS.
Petri nets can't model very much. You can add two numbers or compute their minimum but not multiply two numbers or compute their maximum. In other words, they're not Turing complete. This means that certain properties are decidable! You can algorithmically determine if a net has a token bound or not and in theory even determine if a specific configuration is reachable.6
The problem is that modeling anything with nets is a huge chore, and any addition that makes it less of a chore is exceedingly likely to make it Turing complete. Nonetheless, there are some popular extensions, the most notable of which are "colored petri nets" where places can hold values besides "number of tokens". The main tool for that CPN Tools. I believe Statebox is also trying to use Petri nets as a formal modeling tool.
I really like Petri nets. They aren't very useful for modeling, but they're a fun puzzle. How do you model $BASIC_SYSTEM with just petri nets? How do you make the graph look nice? I like this book on them.
7. Diagram-first
Everything discussed so far was based on mathematical constructs turned into modeling notations. The majority of specification languages were invented elsewhere and used as thinking and communication aides. Almost universally these are diagrammatic notations, and any formal semantics comes later. The first flow chart shares very little in common with the notations people converged on 20 years later.
Which brings us to the most popular formal specification language: UML. More people have drawn sequence diagrams than have used all of the other methods, combined. UML wasn't so much its own language as a compromise between three different diagram notations that tried to guarantee backwards compatibility with all of them. That ones one of the things that ultimately hindered its adoption. SysML is a project to make something similar to UML that's grounded in formal semantics.
Similarly, the C4 architecture model is intended as a means of communicating and documented large scale architecture. Nobody's trying to formally verify them yet but if it sticks around long enough, that very well may happen.
Miscellaneous
Things I left out:
- Dynamic logic, which is a modal logic that's not exactly a temporal logic. The only dynamic logic SL I know off the top of my head is KeyMaeraX.
- SLs that are embedded in a programming language and specifically designed to model systems that will eventually use that language. Examples: Stateright and Spectacle.
- Fault, BPMN, VDM, CADP, LOTOS...
- How people in hardware do formal methods
- Whatever they're doing in the blockchain space, I know nothing about the blockchain space
What to do with this
Like with programming, learning SLs that use different mixes of formalisms is a mind-opening experience that will make you better at specification. Unlike with programming, being better at specification isn't that important. Nobody's going around telling people that state machines are a dead-end and process calculi are the future. It's all this mishmash of different ideas slammed together to make something good for modeling real systems. Learn whichever specification language your friends and coworkers already know, and if you're the first, learn whichever looks the coolest to you.
My main takeaway is that I should get around to learning SPIN.
TLA+ Workshop
This upcoming Monday! Use the code C0MPUT3RTHINGS for 15% off.
(After this week I have one more workshop in June and then I can finally stop pitching this in newsletters. I'm excited to be done. I do not enjoy putting these adverts in my newsletter.)
Update for the Internets
This was sent as part of an email newsletter; you can subscribe here.
-
Originally this was "tree" (as in biological tree), but readers (quite reasonably) thought I meant "hierarchy" trees. ↩
-
Though I did get paid once to write a minizinc constraint model, which was pretty cool ↩
-
Promela is the modeling notation, SPIN is the model checker. The website and official book are both named after SPIN, so that's what I'll use. ↩
-
Technically these are "heterogeneous relationships", as relationship usually means a relationship inside the same set. ↩
-
The example above was kinda drawn from Promela syntax, but I don't actually know it and free-versed a bunch ↩
-
In theory. In practice the reachability problem is, I kid you not, Ackermann-Complete. ↩
If you're reading this on the web, you can subscribe here. Updates are once a week. My main website is here.