The Capability-Tractability Tradeoff
The more you can say, the less you can say about what you can say.
TLA+ Workshop + Review
I'm running a TLA+ Workshop in May! Use the code C0MPUT3RTHINGS for 15% off. As part of the purchase, I'll do a spec review of a spec you write after the workshop. As an example, here's a 1-hour review I did of a spec from February cohort. Thanks to Cory Myers for letting me share the review!
The Capability-Tractability Tradeoff
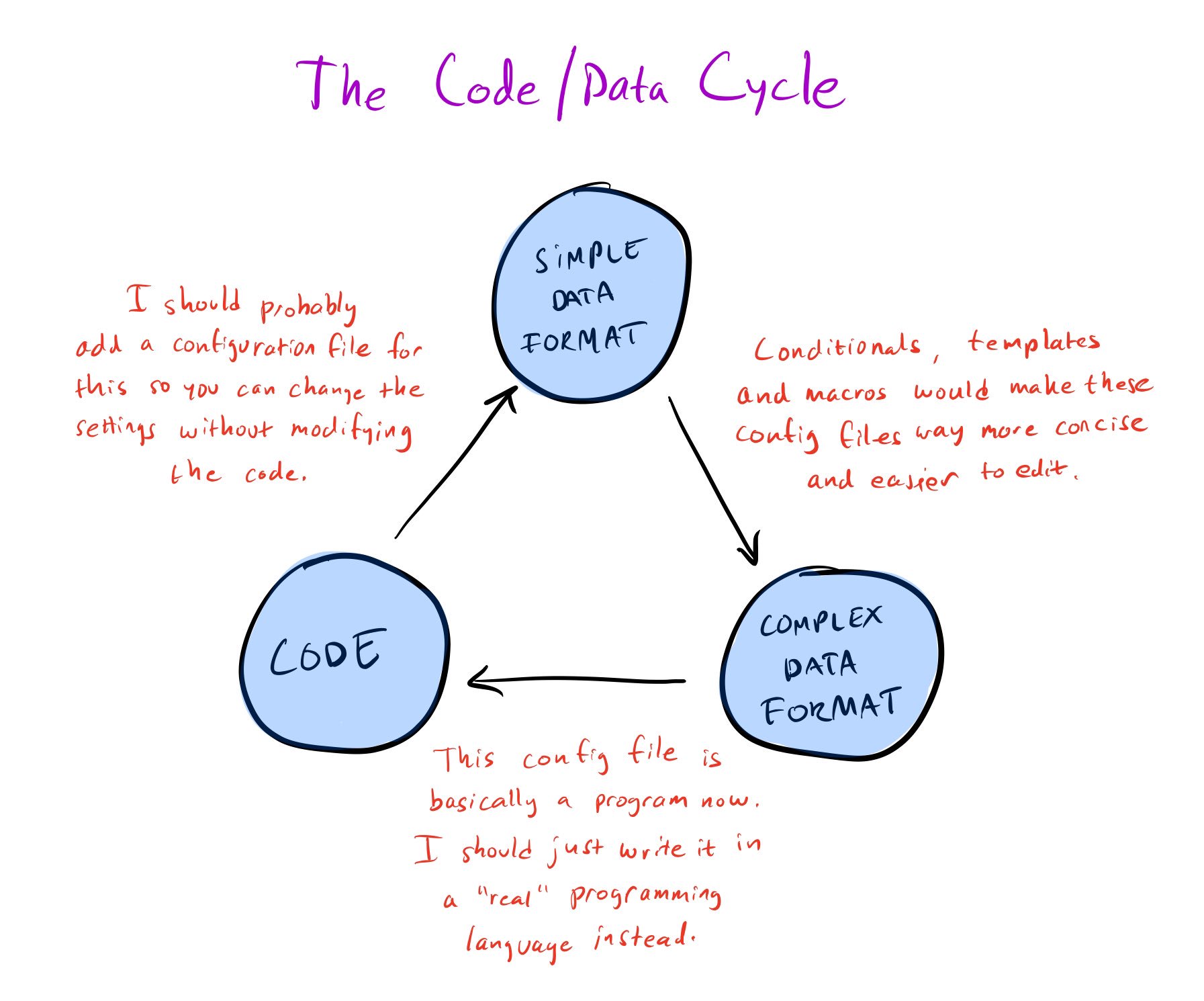
The more things your system can represent, the less you can say about the things that are represented.
ie, if you store strings as ASCII then you can't represent "∀∃🦔", while if you store strings as Unicode then the string's length isn't well-defined. We'll say that Unicode is more capable while ASCII is more tractable.
This is one of the most important tradeoffs in CS, up there with space-time tradeoffs. It has a pretty simple reason, too: the more things your system can represent, the fewer things they all have in common, and the more likely any assertion about that set will have a counterexample.
The canonical example is the computability hierarchy. The Church-Turing claims that a Turing machine is the most powerful kind of automata: if a decision problem (a problem with a "yes/no" answer) cannot be computed by a Turing machine, it cannot be solved by any realizable computational system. The halting theorem says that there's no algorithm which can determine if an arbitrary Turing machine halts on an arbitrary input.1
Turing machines are both capable and intractable. The Pushdown Automata (PDA) is a weaker system that can't compute every decision problem, but they are always guaranteed to return yes/no for every input. More tractable, less capable. At the bottom of the hierarchy is the Deterministic Finite Automata (DFA), which can only compute a very restricted set of problems, is even more tractable than a PDA. 2
That's where the idea is most well-known, but there are other examples as well. Rust's type system is sound: a compiled Rust program is guaranteed to not have type errors. But all sound type systems are also incomplete, meaning there are valid programs that the Rust compiler might reject. With Python, on the other hand, you can type anything as anything and it won't complain up until you try to get the employee_id field from a datetime. This means that Python is more capable and less tractable than Rust: it can represent a wider range of well-typed programs, but there's no guarantee that any given Python program is well-typed.
But wait, there are also many Rust programs that cannot be represented in Python! Specifically, anything involving memory manipulation. Python does not have a concept of a memory address, much less a pointer to one! It also does not have a concept of a memory bug. Rust is more capable and less tractable than Python: it can represent a wider range of memory-manipulating programs, but there's no guarantee that any given Rust program is memory-safe.3
So we have to talk about capability and tractability with respect to a property or class of representations. It's a little closer to a lattice than a spectrum. Other examples of capability/tractability tradeoffs:
- Tag systems
- Linked lists -> trees -> DAGs -> directed graphs (with cycles)
- The data you can encode in JSON vs YAML vs XML vs a SQL database.
- Constructive data is more tractable, predicative data is more capable.
- SAT solving is much easier than SMT or constraint solving, but also encodes fewer problems.
- Static analysis is a lot easier when your language doesn't have macros, introspection, or metaprogramming.
This also applies to things outside of CS! In math, complex numbers are a superset of the reals, but reals are totally ordered and complex numbers are not.
As a tradeoff
Sometimes a "tradeoff" has a predisposition, like "Tractability is more important but sometimes you have to consider capability." I don't know if that works here; it seems like this is a tradeoff you always have to think about. Tractability seems more important, in that once you have enough capability in your system to cover your use case, you don't need more of it. But there are other considerations too:
- Requirements change, and your system might not be capable enough to handle the change.
- Backwards compatibility makes it easier to add features, which trades tractability for capability, than remove features, which goes the other way.
- If you make a system more capable, you might break tractability assumptions other parts of the system relied on, and so introduce bugs.
- You can use a subset of a capable system to keep things tractable, and you can use mimicry to make a tractable system more capable.
- Not every change is zero-sum: we sometimes discover new techniques that make systems more tractable/capable for "free".
Basically it's something you gotta think about per project.
Note that capability and tractability are independent of ergonomics, how easy it is to actually express or analyze something. Usually ergonomics ends up trading off with the other two but it's not required to.
-
There's a common misconception that the halting problem is only of theoretical interest, because physical computers have finite states and so must always halt. But a corollary of the halting problem is "there's no algorithm which can tell if an arbitrary machine halts on an arbitrary input before hitting the memory limit". Similarly, you can't cheat the halting problem with timeouts, either. ↩
-
For a given DFA we can determine the exact set of inputs it accepts, which is undecidable with PDAs. ↩
-
There's that whole "borrow checker" thing Rust is known for, but there's one flaw:
unsafe. WithoutunsafeRust isn't capable enough to compete with C. ↩
If you're reading this on the web, you can subscribe here. Updates are once a week. My main website is here.